Als "Turing-Maschine" wird gemeinhin ein von A.Turing erfundener "Formalismus" bezeichnet, mit welchem sich jeder Algorithmus quasi konstruktiv beschreiben lässt. A.Turing publizierte den Formalismus 1936 in einem Artikel "On Computable Numbers, with an Application to the Entscheidungsproblem", wo er selbst den Ausdruck "automatisches Maschine" verwendet. Der Ausdruck "Turing-Maschine" wurde 1937 zuerst von A. Church im Journal of Symbolic Logic verwendet. Die Turing-Maschine ist ein Kalkül. A. Church hat mit A. Turing zusammen gezeigt, dass sie äquivalent zum Lambda-Kalkül ist.

Die Turing-Maschine ist keine Maschine, noch nicht einmal die Beschreibung einer Maschine, sondern ein formalsprachliche Beschreibung eines Verfahrens zur Analyse von Algorithmen. A. Turing behandelt in seinem Aufsatz ein mathematisches Problem, es geht ihm nicht um die Konstruktion einer Maschine. Er beschreibt anhand einer Pseudo-Maschine eine Klasse von Entscheidungsproblemen mit algorithmischen Lösungen, um zu zeigen, dass es Entscheidungsprobleme gibt, die sich algorithmisch nicht lösen lassen.

A. Turing beschreibt ein Berechnungs-Verfahren in Form von elementaren Operationen, was ihn in einem Umkehrschluss dazu veranlasste - metaphorisch - von einer Maschine zu sprechen, weil wirkliche Maschinen Operationen verkörpern. [ On Computable Numbers Volltext ] Auszug: 2. Definitions. Automatic machines. If at each stage the motion of a machine (in the sense of §1) is completely determined by the configuration, we shall call the machine an “automatic machine” (or a-machine). For some purposes we might use machines (choice machines or c-machines) whose motion is only partially determined by the configuration (hence the use of the word “possible” in §1). When such a machine reaches one of these ambiguous configurations, it cannot go on until some arbitrary choice has been made by an external operator. This would be the case if we were using machines to deal with axiomatic systems. In this paper I deal only with automatic machines, and will therefore often omit the prefix a-. Computing machines. If an a-machine prints two kinds of symbols, of which the first kind (called figures) consists entirely of 0 and 1 (the others being called symbols of the second kind), then the machine will be called a computing machine. If the machine is supplied with a blank tape and set in motion, starting from the correct initial m-configuration, the subsequence of the symbols printed by it which are of the first kind will be called the sequence computed by the machine. The real number whose expression as a binary decimal is obtained by prefacing this sequence by a decimal point is called the number computed by the machine. At any stage of the motion of the machine, the number of the scanned square, the complete sequence of all symbols on the tape, and the m-configuration will be said to describe the complete configuration at that stage. The changes of the machine and tape between successive complete configurations will be called the moves of the machine. {233}

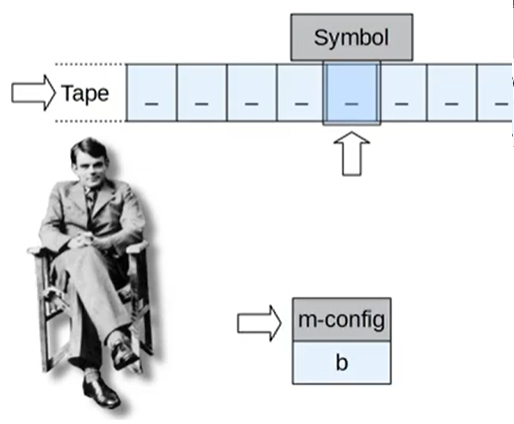
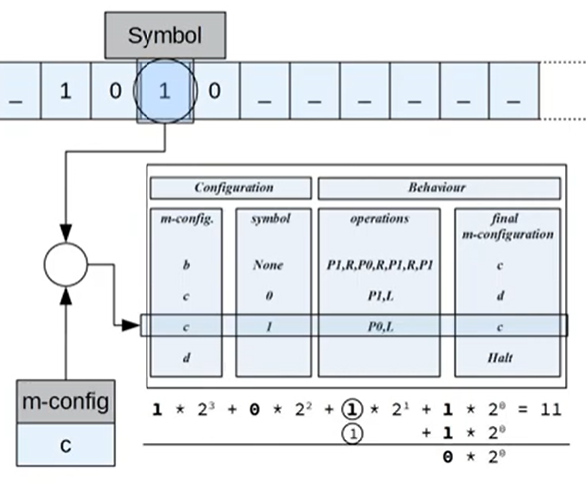
Eine sehr anschauliche Erläuterung: Bildquelle: Michael Holzheu

Circular and circle-free machines.

If a computing machine never writes down more than a finite number of symbols of the first kind it will be called circular. Otherwise it is said to be circle-free. A machine will be circular if it reaches a configuration from which there is no possible move, or if it goes on moving, and possibly printing symbols of the second kind, but cannot print any more symbols of the first kind. The significance of the term “circular” will be explained in §8.

Hinweise:

Die Beschreibungen im Formalismus "Turing-Maschine" entsprechen Programmen, die auf der universellen Turing-Maschine ausgeführt werden können. Eine anschauliche Darstellung dieser "Maschine" ist in Weizenbaums Macht und Ohnmacht:81 ff. Eine weitere Veranschaulichung bietet der folgende Link: http://cgi.student.nada.kth.se/cgi-bin/d95-aeh/get/umexeng.

Das mathematische Konzept der "Turing-Maschine" beschreibt die Steuerung einer Maschine, keine Maschine. Die Steuerung ist universell, jede Maschine ist speziell. "Universell ist die Turing-'Maschine' lediglich als Steuerungskomponente für Maschinen" (Todesco: Technische Intelliegenz:84).

"Die sogenannte universale Turingmaschine ist wie alle Turingmaschinen als eine Folge von Quintupeln beschreibbar, (...): (augenblicklicher Zustand, gelesenes Symbol, nächster Zustand, geschriebenes Symbol, Richtung der Bandbewegung) und diese Quintupel können ihrerseits in der Sprache geschrieben werden, auf die die Turingmaschine eingestellt ist. Die universale Turingmaschine ist infolgedessen in der Lage, eine Beschreibung von sich selbst zu verarbeiten und sich selbst zu imitieren" ( Weizenbaum:92).

Die Konfusion ist belieb gross und wurde natürlich nicht durch Turing begründet. Seine Formalismus wird in der Konfusion nur immer wieder zitiert, weil er Ausdruck dieser Konfusion (Fusion zwischen Mensch und Maschine) ist.

In "Konstruktion der Wirklichkeit"(Einführung in den Konstruktivismus:60) verwendet Heinz von Foerster die Turing-"Maschine" zur Erläuterung der trivialen Maschine.

Stellen aus Todesco: Technische Intelligenz

Damit war die sogenannte Turing-Maschine, die einen universellen Steuerungsmechanismus darstellt, im wesentlichen gebaut. Entsprechend äusserten die Erbauer von ENIAC in der Zeitung "Prisma" vom November 1946: "Bei der Konstruktion von ENIAC wurden manche Erfahrungen gewonnen, die es ermöglichen werden, in Zukunft ähnliche Maschinen kleiner und einfacher auszuführen. Keinesfalls wird es aber gelingen, elektronische Rechenmaschinen zu bauen, die mehr leisten als ENIAC, denn bisher hat man trotz aller Bemühungen noch keine einzige noch so komplizierte mathematische Aufgabe gefunden, die ENIAC nicht einwandfrei gelöst hat" (zit.in: Weiss,1983,17). Diese etwas unverschämt anmutende Äusserung ist in gewisser Hinsicht korrekt. Die Computer der "nullten" Generation sind bereits eigentliche Automaten. Wir nennen sie Turing-Maschinen, weil A.Turing eine mathematische Theorie geliefert hat, die formal nachweist, dass diese Maschinen die Transformationsregeln jeder formalen Sprache verkörpern können, weil sie ihrerseits auf einer "universellen Maschine" beruhen, die alle steuerbaren Automaten simulieren kann (59). 83

Mit seiner ideellen "Maschine" zeigte A.Turing, dass sich mathematische Abstraktionen in Maschinen begründen. Insbesondere hat A.Turing mit seiner Maschine den Begriff des Algorithmus, der zuvor für rechnerische Verfahren insgesamt verwendet wurde, spezifiziert (60). Ein eigentlicher Algorithmus (effektives Verfahren) ist eine abstrakte, vollständige Beschreibung eines Maschinensteuerungsprozesses (61). Hinter jedem Algorithmus steckt die Steuerung einer wirklichen Maschine. 83

Selbstverständlich gibt es keine Allzweckmaschine. Universell ist die Turing-"Maschine" lediglich als Steuerungskomponente für Maschinen. Im gleichen Sinne könnte man auch den Otto-Motor als universelle Maschine bezeichnen, weil er als Antriebs-"Maschine" alle wirklichen Maschinen antreiben kann. 84

J. von Neumanns Beschreibung hat deshalb eine enorme praktische Bedeutung, während A. Turings Maschine "nur" theoretisch interessant war. Dem Theoretiker gilt deshalb Turings, dem Praktiker von Neumanns Beschreibung als entscheidender Durchbruch: ”Es war einer der grössten Triumphe der menschlichen Intelligenz, als 1936 der englische Mathematiker Alan M.Turing beweisen konnte, dass der Bau einer solchen Maschine möglich ist” (Weizenbaum, 1978, 88); ”Hier erfolgte der bahnbrechende Schritt, den John von Neumann in einer genialen Abstraktion des Steuerungsprozesses vollzog” (Weiss, 1983,15). G. Révész schreibt in einer Von-Neumann-Biographie gar: ”Die Turing-Maschine ist eine rein mathematische Abstraktion, die wegen ihrer Primitivität für den praktischen Gebrauch absolut ungeeignet ist” (Révész,1983,100).

Literatur

Vgl. Keil-Slawik, 1992, 155, 180
Vgl. Krämer, 1988, 169f.

Die sogenannte Turing-Maschine in kybernetiks

Als "Turing-Maschine" wird gemeinhin ein von A.Turing erfundener "Formalismus" bezeichnet, mit welchem sich jeder Algorithmus quasi konstruktiv - als Folge von Operationen - beschreiben lässt. A.Turing publizierte den Formalismus in einem Artikel "On Computable Numbers, with an Application to the Entscheidungsproblem", wo er selbst den Ausdruck "automatisches Maschine" verwendet. Der Ausdruck "Turing-Maschine" wurde 1937 zuerst von A. Church in Journal of Symbolic Logic verwendet.

Die Turing-Maschine ist keine Maschine, noch nicht einmal eine Beschreibung einer Maschine, sondern ein formalsprachliche Beschreibung eines Verfahrens zur Analyse von Algorithmen. A. Turing behandelt in seinem Aufsatz ein mathematisches Problem, es geht ihm nicht um die Konstruktion einer Maschine. Er beschreibt anhand einer Pseudo-Maschine eine Klasse von Entscheidungsproblemen mit algorithmischen Lösungen, um zu zeigen, dass es Entscheidungsprobleme gibt, die sich algorithmisch nicht lösen lassen.

A. Turing beschreibt ein Verfahren in Form von elementaren Operationen, was ihn in einem Umkehrschluss dazu veranlasste - metaphorisch - von einer Maschine zu sprechen, weil "wirkliche" Maschinen in dem Sinne Operationen "verkörpern", als ich die Maschinenzustände, die die Maschine durchläuft, als Variablenwerte sehen kann. J. Weizenbaum hat die "Turingmaschine" sehr schön dargestellt: Ein Mensch, der mit einer Rolle WC-Papier und einer Handvoll Steine spielt.

In einem für "Turingmaschinen" typischen Artikel (http://www.nzz.ch/aktuell/digital/das-gadget-aller-gadgets-1.17262673) schreibt beispielsweise S. Betschon in der NZZ: "Der erste moderne Computer, eine universell programmierbare Maschine, fähig zur Lösung äusserst komplizierter mathematischer Probleme, wurde Ende 1936 in Betrieb genommen. ... Bis heute gibt es keine, die sie an Leistung übertreffen könnte. ... Die Rede ist von der Turingmaschine. ... Kein Smartphone ... kann die Turingmaschine übertreffen."

Der begriffliche Wirrwarr, der eine formalsprachliche Beschreibung mit einem Smartphone so vergleicht, dass das eine das andere übertreffen kann, widerspiegelt sich in der naiven Vorstellung, wonach A. Turing das Denken beschreibt: "Turing zergliedert Denkprozesse, versucht, sie so sehr zu zerkleinern, dass sie sich nicht mehr weiter zerkleinern lassen. Er möchte zu den Grundbausteinen, den Elementarteilchen, des Denkens vordringen. Er möchte das, was im Kopf des Rechnenden vor sich geht ... lückenlos und genau erfassen." Was A. Turing tatsächlich beschreibt, ist ein Spiel, bei welchem Gegenstände bewegt werden, wie sie wohl in keinem Kopf vorkommen. Ob der Spielende dabei denkt, ist für das Spiel ganz ohne Bedeutung, was sich darin zeigt, dass der Spielprozess als mechanischer Prozess konzipiert ist.

Die sogenannte Turing-Maschine wird immer wieder bemüht, wenn gezeigt werden soll, dass "geistige Arbeit" mechanisierbar sei. S. Betschon bringt das verblüffend simpel auf den Punkt: "Es ist eine verblüffend simple Maschine, die sich Turing als Ersatz für den Menschen ausgedacht hat." Maschinen ersetzen Menschen - er lässt offen, wo und für wen das der Fall ist.

Jenseits von schwachem Sinn kann man über das Verhältnis von Mathematik und Maschinenbau im Sinne von Technik nachdenken. A. Turing hat dazu - wie bewusst auch immer - auf der Seite der Mathematik einen wichtigen Beitrag geliefert. Sagen, er habe eine Maschine gebaut, kann aber nur, wer Maschinen als geistig-feinstoffliche Wesen sieht, die beispielsweise Rechnen können.

Lange vor A. Turing gedenkt hat, haben andere Menschen wirkliche Rechenmaschinen gebaut. Um ein berühmtes Beispiel zu nennen, C. Babbage hat eine Maschine hergestellt, die er als analytische Maschine bezeichnete, weil er damit Rechnen wollte. Die Maschine von C. Babbage wurde nicht aus mathematischen Gründen nie fertiggestellt, sondern weil die Herstellungstechnik, also die Werkzeuge nicht hinreichend entwickelt waren. K. Zuse, der etwa zeitgleich wie A. Turing - einfach für die andere Kriegspartei - arbeitete, hat beispielsweise eine Rechenmaschine gebaut, von der man vernünftigerweise sagen kann, dass sie in Betrieb genommen wurde.