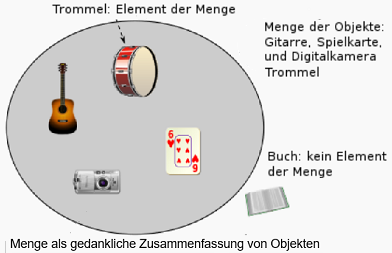
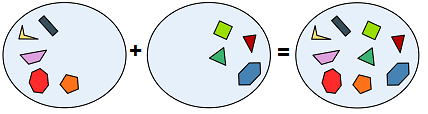
Den Ausdruck "Menge" verwende ich im Alltag sehr vielfältig und meine damit meistens ein nicht weiter spezifiziertes, oft zählbares oder volumenhaftes Ausmass, das ich auch mit viel oder sehr viel bezeichne. Ich spreche etwa von einer Menschenmenge oder sage, dass ich eine Menge Bier getrunken oder eine Menge Arbeit vor mir habe. Der Ausdruck "Menge" ist problematisch, weil er in der Mathematik (Mengenlehre) und in der Physik (Molmenge) und im Alltag (Anzahl oder Volumen) ganz verschieden verwendet wird. Homonyme sind bei weitem nicht immer problematisch, aber in diesem Fall herrscht viel Konfussion, weil Menge oft auch mit Grösse oder Masse verwechselt wird. Im Karlsruher Physikkurs ist - ziemlich ungeschickt - von einer mengenartigen Grösse die Rede.

Die mathematische Menge

Den Ausdruck "Menge" verwende ich mathematisch zur Gruppierung von - im Prinzip (auch nicht)-zählbaren - Entitäten (Elemente). Ich sage etwa die Menge der Primzahlen, und kann dann sagen, welche Zahlen zur Menge gehören und welche nicht. Und ich kann über die Mächtigkeit der Menge sprechen, womit ich die Anzahl der Elemente bezeichne. Diese Verwendung des Ausdruckes "Menge" begründet die Mengenlehre von G. Cantor.

Bildquelle: Wikipedia

"Eine Veranschaulichung des Mengenbegriffs, die Richard Dedekind zugeschrieben wird, ist das Bild eines Sackes, der gewisse (als Einzelne abgrenzbare) Dinge enthält. Nützlich ist diese Vorstellung zum Beispiel für die leere Menge: ein leerer Sack. Die leere Menge ist also nicht „nichts“, sondern der Inhalt eines Behältnisses, das keine der für es als Inhalt vorgesehenen Dinge enthält. Das „Behältnis“ selbst verweist nur auf die bestimmte zu zählende Sorte und Art von Elementen.
Die leere Menge ... führt das "nicht" ein. Zwei Aepfel, ein Apfel, k(nicht)ein Apfel ...
Die "leere Sack-Vorstellung" taugt auch im Kindergartenunterricht.

Die Mengenlehre wurde kritisiert von B. Russell, in der Typentheorie, die Klasse und Menge unterschied (aber in der Mathe keinen Erfolg hatte) und durch E. Zermelo, der heute allgemein gilt. Beide erkannte eine Art Paradoxie, die sie mit einer Menge, die sich selbst (nicht) enthält verbunden haben - obwohl es in deren Theorie keine Menge, die sich selbst enthält.

Es gibt zahlreiche populäre Varianten der Russellschen Antinomie. Am bekanntesten ist das Barbier-Paradoxon, mit dem B. Russell selbst 1918 seinen Gedankengang veranschaulichte und und seine Typentheorie begründete: "Der Mann, der alle Männer im Dorf rasiert, die sich nicht selbst rasieren."
Das wird mithin als logisches Problem bezeichnet, aber es bleibt unklar, wovon die Rede ist, resp. was die bezeichnete Menge ist.

[ Warum die ''Menge aller Mengen'' ein widersprüchliches Konzept ist ]

Die physikalische Menge

Den Ausdruck "Menge" verwende ich physikalisch - ganz unabhängig von der mathematischen Deutung - für die Grösse Stoffmenge, also für die einzige zählbare Basisgrösse.

Die umgangssprachliche Menge

Die umgangssprachliche Menge wird sehr oft auch in der Mathematik und in der Physik verwendet und oft mit Grösse verwechselt:

In der Mathematik wird oft von einer Grösse gesprochen, wenn der Wert einer Variablen gemeint ist. Als Grösse gilt dann eine Zahl vor/mit einer Einheit, was einer umgangsprachlichen Menge entspricht: 20 Liter.

Physiker verwenden den Ausdruck Menge oft in umgangssprachlichen Verkürzungen. Sie sprechen etwa von einer bestimmten "Menge Energie" (wobei sie allerdings auch den Ausdruck Energie umgangssprachlich verwenden) und bezeichnen damit (wie die Mathematiker) eine Zahl mit einer Einheit: Er hat 20 Joule verbraucht. 20 bezeichnet in dieser Redeweise die Grösse einer Menge. Das entspricht der Alltagssprache, verletzt aber die Begriffe der Physik.

Meine Physik

Es geht dabei nicht um die richtige Verwendung von Wörtern, sondern darum, wie sie vereinbart werden. In meiner Physik geht es um die Tätigkeit des Messens. Welche Wörter ich wie verwende, erläutere ich anhand der Messoperation.

In einem Fluss fliesst eine bestimmbare Menge Wasser, die ich - beispielsweise in Litern - messen kann. Dabei verwende ich die Grösse Volumen.
die Messoperation besteht hier darin, das Wasser in Gefässe abzufüllen und die vollen Gefässse zu zählen. Menge verwende ich also in einem umgangssprachlichen Sinn, der hier spezifiziert ist.

Das Wasser füllt oder hat ein Volumen. Das Wasser hat auch ein Gewicht. Ich kann es also auch wägen, was eine andere Art des Messens ist.

Ich kann aber auch etwas ganz anderes messen. Ich kann messen, wie schnell das Wasser fliesst oder welche Energie im Fliessen des Wassers enthalten ist. Auch in diesen Fälle verwende ich Messoperationen, die ich erläutern kann.

Die Geschwindigkeit des Wassers in einem Fluss ist eine komplizierte Sache. Erst durch die Messoperation wird bestimmt, was ich in diesem Fall als Geschwindigkeit bezeichne.
Das Wort Geschwindigkeit die indem Sinne als Energie- oder Entropie-TRÄGER fungiert, als ich MESSEN - also eine Gösse einführen - kann, wie gross die EnergieMENGE ist.

statt von von einer bestimmten Anzahl Joule oder Kalorien.

siehe auch imaginäre Menge